출처 : youtu.be/6Iq5iMCVsXA
근본없이 딱히 이론을 하나하나 뜯어보지 않고 공부했던 탓인지 면접 준비함에 있어서 가장 기본적인 이론이 부족해서 공부를 하는 중에 알맞은 강의가 있어서 워드에 정리하고 복습할겸 다시 업로드 중이다.
해당 유튜브 컨텐츠에 나온 설명을 기준으로 다시 재정리해서 복습하기 위함이다.
시간 복잡도에 있어서 대표적으로 거론되는 몇개가 정리되어 있는데,
O(1) , O(n) , O(n^2) , O(nm) , O(n^3) , O(2^n) = Fibonacci , O(mn) , O(log n) , O(sqrt(n))
이정도가 정리되어 있다.
1. O(1)
: 입력 데이터에 상관없이 언제나 일정한 시간이 걸리는 알고리즘

데이터가 증가함에 따라 성능에 변함이 없다.
2. O(n)
입력 데이터에 크기에 비례해 처리시간이 걸리는 알고리즘

데이터가 증가함에 따라 비례해 처리시간도 같이 증가
For(int[] n)
{
For I = 0 to n.length
}
언제나 같은 비율로 증가
3. O(n^2)
n으로 루프를 돌리면서 안에서 또 n으로 루프를 돌릴떄
예로들어 2중 for문에서 i와 j를 n값을 받아와 중첩으로 돌릴 때

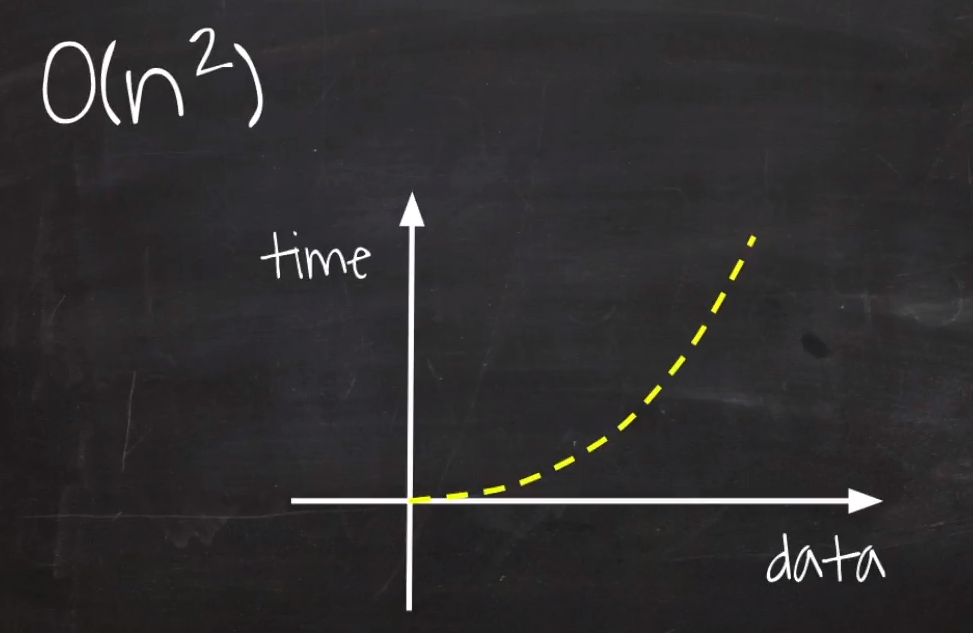
데이터가 커지면 커질수록 처리시간의 부담이 점점 커진다.
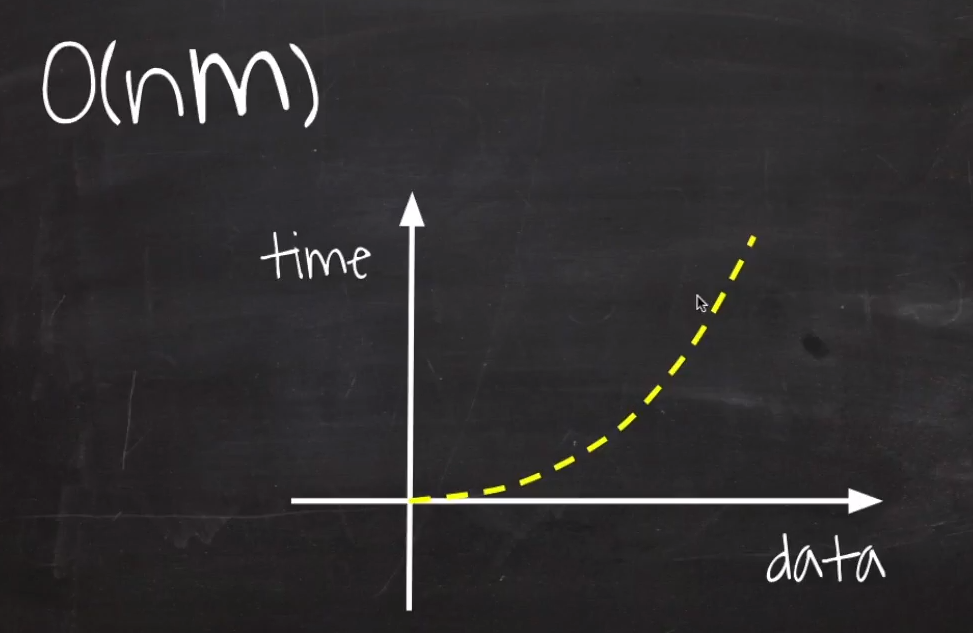
4. O(nm)
N을 m만큼 돌리는것.
N^2와는 명백히 다르다.
빅오에선 정확한 값이 아닌 추정치를 계산하기 위함이기에 n과 m의 값의 차이에 별 상관 없이 그래프로는 O(n^2)과 같이 표기한다.

5. O(n^3)
N을 가지고 3중으로 돌린 경우
대략 n차원 배열이라 생각하면 된다.
N^2의 경우 형태가 2차원 배열이고 n^3의 경우 당연히 정육면체 모양이 나온다.

늘어날때마다 가로 세로 높이가 계속 늘어나서 O(n^2)보다 더욱 급격하게 휜다.
6. O(2^n)
Fibonacci Numbers를 떠올리면 된다.
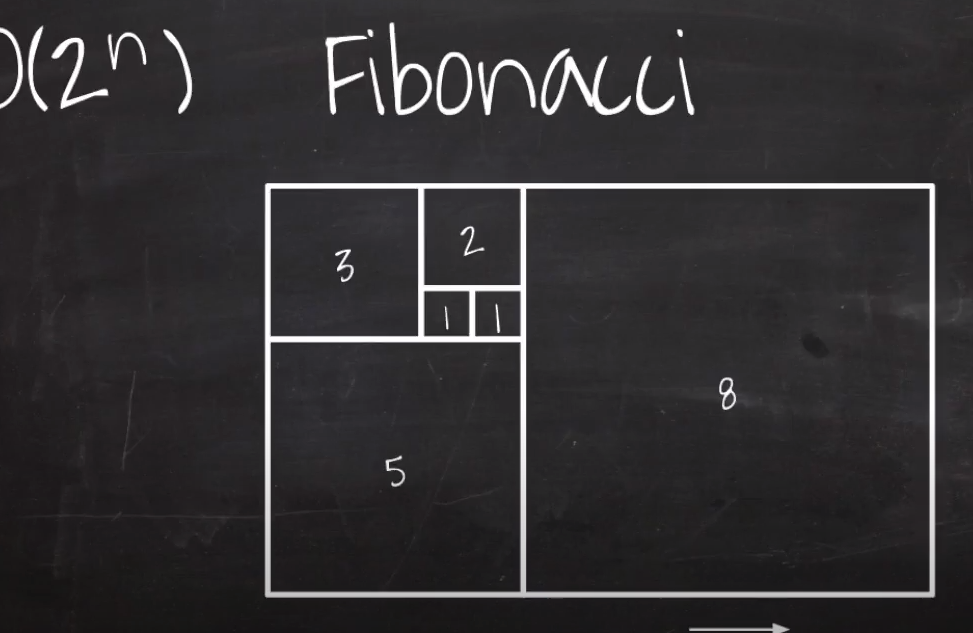

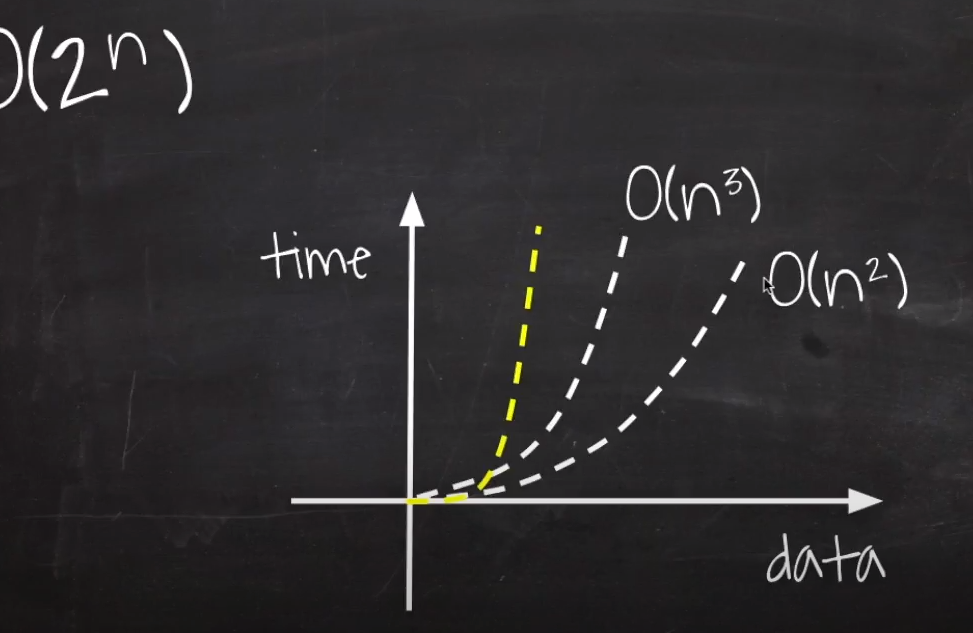
기하학의 황금비율 나선형 그래프가 나온다.
피보나치수열은 이전의 숫자와 그 이전의 이전의 숫자를 알아야한다.
즉 n-1 | n-2의 값을 알아야한다. 이건 아는 내용이니 패스
7. O(log n)
대표적인 알고리즘은 이진 검색
예로들어 탐색시 키 값을 하나 정한 후 배열의 가운데 값을 찾는다.
1 2 3 4 5 6 7 8 9 | key : 6
처음 5를 고른 후 현재 키 값은 6이므로 맨 왼쪽값인 1부터 5까지 제외하고 다시 6 7 8 9 중 중간값인 7을 골라서 키 값과 비교해보면 더 작으므로 앞쪽인 6이 나온다.
이렇게 한번 처리해야할때마다 절반씩 뚝뚝 떨어지는 알고리즘을 O(log n)이라고 한다.
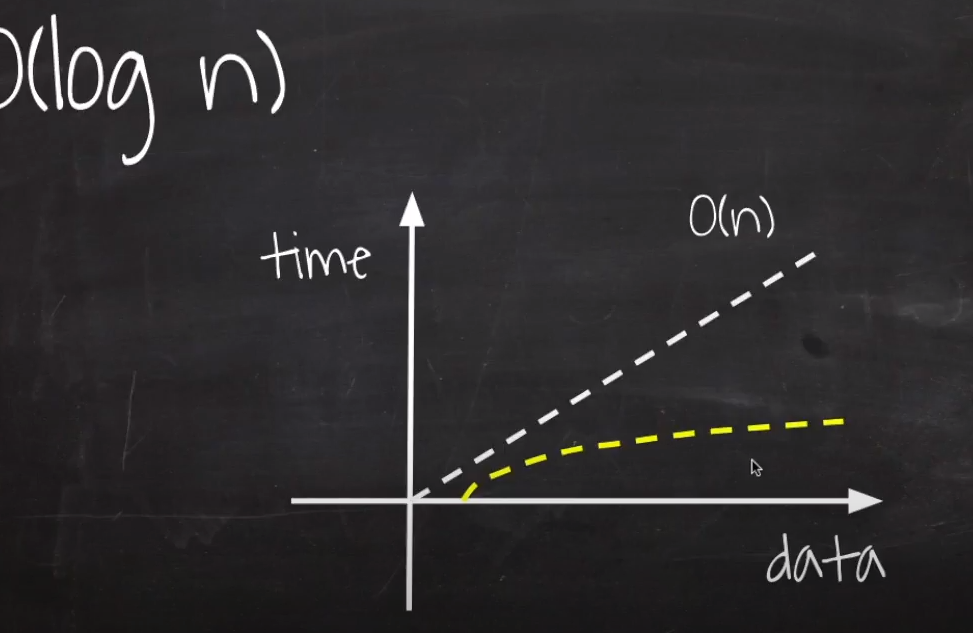
전체값 -> 중간값 -> 중간값+1부터 반복…. -> 결과
데이터가 증가해도 성능에 큰 차이가 없다.
8. O(sqrt(n))
√100 = 10 | √9 = 3
예로들어 n=4라면 정사각형에 채워서 맨 윗줄에 나오는 값이 sqrt(n) = 2
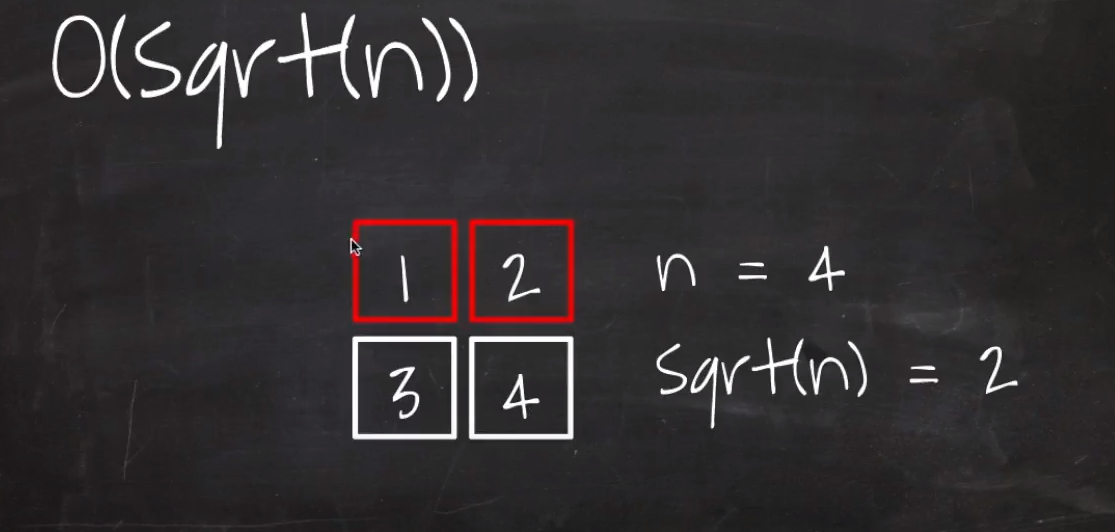


역시나 n이 9일경우 정사각형으로 상자를 배치한 후 맨 위의 값이 제곱근이다.
팁
빅오에선 상수는 과감히 버린다.
O(2n) => O(n)으로 표기한다.
실제 알고리즘의 러닝타임이 아닌 장기적으로 데이터가 증가함에 따른 처리시간의 증가율을 표기하기 위함이기 때문에
O(n^2 + n^2) => O(n^2)
'# 공부 > # 알고리즘' 카테고리의 다른 글
| [스택] 백준알고리즘 10828번 c++ (0) | 2021.01.17 |
|---|---|
| [정렬] MergeSort 병합정렬 (0) | 2021.01.16 |
| Procedural Dungeon Generation in Unity #2 (0) | 2020.07.24 |
| [완성] Procedural Dungeon Generation (0) | 2020.07.14 |
| [No. 1011] C++ Fly me to the Alpha Centauri 문제 해설 (0) | 2020.06.16 |


